The energy density and the full energy:
(1.1)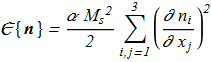
(1.2)
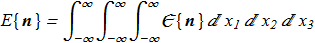Unit vector field
(1.3)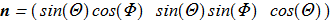
(1.4)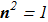
Euler-Lagrange equations for {1.1} :
(1.5)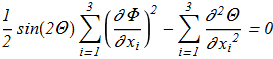
(1.6)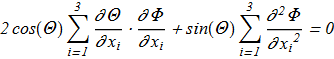
Even if we assume that there are localized solutions with finite energy
(1.7)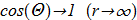
then it follows from the equations, the solutions will also be all sorts of functions
(1.8)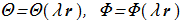
with energy
(1.9)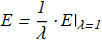
It follows that the size of the soliton is not fixed and is proportional to its energy, and there are no reasons preventing a shrinking of the soliton. In other words we can say that the size of the soliton is not defined by the parameters of the system. In fact, for solutions of the equations {1.5}-{1.6}, the energy will always be infinite.
Let's turn to the dynamic case. Landay-Lifshitz equation:
(1.10)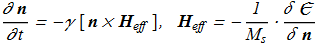
in expanded form:
(1.11)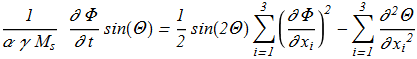
(1.12)
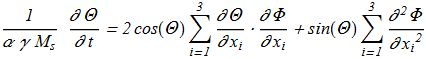The equation {1.10} allows a uniformly moving soliton with a stationary profile and a uniform precession frequency:
(1.14)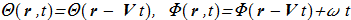
In the following we will mean
(1.15)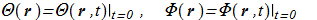
Governing equations:
(1.16)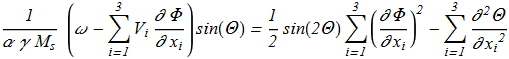
(1.17)
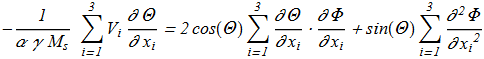In this case, there is a required scale constant:
(1.18)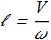
The equations {1.16}-{1.17} can be simplified for the case of axially symmetric solitons propagating along the axis of precession:
(1.19)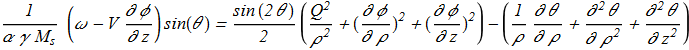
(1.20)
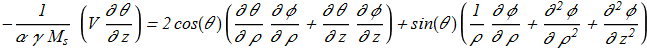where
(1.21)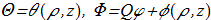
in cylidrical coordinate system (ρ,φ,z);
(1.22)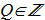
New functions {1.21} can be represented by a new unit vector field:
(1.23)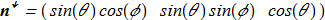
(for details, see Faddeev model). If the Hopf index is not zero, then such soliton = hopfion.
In work [N. Papanicolaou, T.N. Tomaras "Dynamics of magnetic vortices", Nuclear Physics B 360, (1991) 425 ref] the authors found a new formula for calculating the momentum vector P of the magnetization field:
(2.1)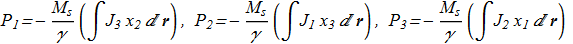
where
(2.2)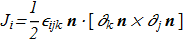
where Levi-Civita symbol are used, summations over the double indices are assuming. This formula compares favorably with the previously known, as it allows to calculate the momentum if we know only the projections of vectors while the computational complexity does not appear near the poles Θ=0 and Θ=π.
The effective functional will be in form
(2.3)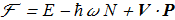
where N are the total number of magnons
(2.4)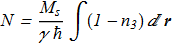
The Euler-Lagrange equations for {2.3}:
(2.5)
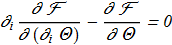(2.6)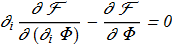
in exactly the same as {1.16} - {1.17}.
In this formulation the problem can be solved numerically by minimizing the energy with the additional constraints on P and N integrals.
Probably, as was announced in [N. Papanicolaou "Dynamics of magnetic vortex rings", NATO Science Series C, Vol. 404 (1993) 151 copy], it is possible to find a solution numerically solving the evolutionary Landau-Lifshitz equation for the initial state in the form of some Hopf fibration. And after the radiation processes, the soliton should stabilize and move without the change of shape.
In [N.R. Cooper " 'Smoke Rings' in Ferromagnets", Phys. Rev. Lett. 82, 1554 (1999) ref; arXiv:cond-mat/9901037v1], the author first obtained the numerical solutions for toroidal hopfions {1.21} with H=1 (Q=1). The problem was solved numerically by minimizing the energy with the additional constraints on P and N integrals. The author has found the parametric dependence of the soliton energy. Calculated energy value depends on the count of grid nodes. This is due to weak localization of the soliton - slowly decreasing power asymptotics.
In [P. Sutcliffe "Vortex Rings in Ferromagnets", arXiv:0707.1383v1; Phys. Rev. B 76, 184439 (2007) ref] was completed three-dimensional numerical minimization, not with an axially symmetric test function. The result was nevertheless a toroidal hopfion H=1 is likely the one of that calculated by N.R. Cooper, but a comparison of energy is absent. The author also studied the evolution (by Landay-Lifshitz) of the soliton and argues that it is stable to perturbations violating axial symmetry.
This page is not complete and if you find inaccuracies, if you have any comments or additional material - do not hesitate to contact us.