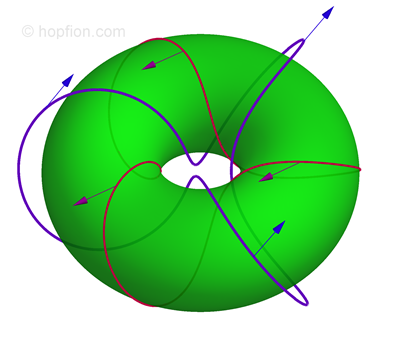
A hopfion (or Hopf soliton) is a topological soliton which is classified by the Hopf invariant and has non-zero Hopf index value. A hopfion is a knot in a three-dimensional continuous unit vector field and cannot be unknotted without cutting. Since hopfions are 3D solitons, their behavior should be similar to particles. However, in addition to this, the total topological charge of the system (total Hopf index) is a constant. Typically, hopfions are described by nonlinear partial differential equations in physical systems and even numerical studies are very difficult.
In theory, the physical nature of hopfions may be different. First of all, the vector field
(1.1)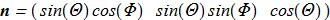
itself may be normalized physical quantity:
(1.2)
Like the normalized magnetization vector in ferromagnetism. Second, the lines of preimages
(1.3)
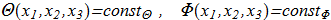of vectors may correspond to physical quantities:
(1.4)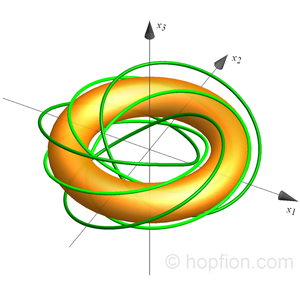
Like electric or magnetic lines of force. It is also possible that these options will only be mathematically related to the actual physical quantities (hidden hopfion).