
Maxwell's equations for the electromagnetic field in vacuum
(1.1)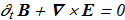 (1.2)
(1.2)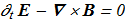 (1.3)
(1.3)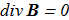 (1.4)
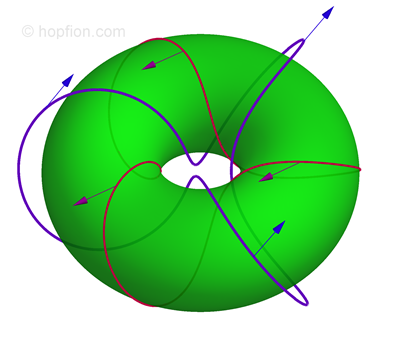
(1.4)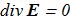 Despite the fact that the equations are linear, an interesting question about the existence of such solutions, when the lines of force remain linked (wiki). And is there a relation between such configurations and hopfions.
Despite the fact that the equations are linear, an interesting question about the existence of such solutions, when the lines of force remain linked (wiki). And is there a relation between such configurations and hopfions.
If A is the magnetic vector potential, then
(1.5)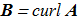 If there are no induced electrostatic fields, and C is the electric vector potential, then
(1.6)
If there are no induced electrostatic fields, and C is the electric vector potential, then
(1.6)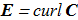 The equations (1.1)-(1.4) are transformed:
(1.7)
The equations (1.1)-(1.4) are transformed:
(1.7)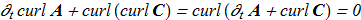 (1.8)
(1.8)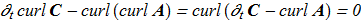 From (1.7)-(1.8) follows
(1.9)
From (1.7)-(1.8) follows
(1.9) (1.10)
(1.10)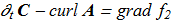 Where f1 and f2 are all possible functions:
(1.11)
Where f1 and f2 are all possible functions:
(1.11)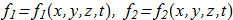
The magnetic helicity and electric helicity are defined as
(1.12)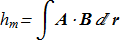 (1.13)
(1.13)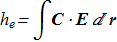 It is easy to verify the relationships
(1.14)
It is easy to verify the relationships
(1.14)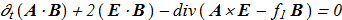 (1.15)
(1.15)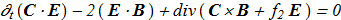 by substituting the time-derivatives from (1.9)-(1.10).
by substituting the time-derivatives from (1.9)-(1.10).
From (1.12)-(1.13) and (1.14)-(1.15) it follows that if the field is localized in space (the vectors B and E are rapidly decreasing at infinity), then
(1.16)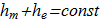 (1.17)
(1.17) From (1.16) and (1.17) the following conclusion:
(1.18)
From (1.16) and (1.17) the following conclusion:
(1.18)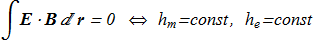
In [A.F. Ranada "A topological theory of the electromagnetic field", Lett. Math. Phys. 18, 97 (1989) ref] it was shown that there are solutions of Maxwell's equations with the structure of hopfion-like type because the helicities (1.12), (1.13) are constants and not zero (an analogy with hydrodynamic helicity assumed). In view of (1.18), this class of solutions has a certain property, namely:
(2.1) In subsequent work [A.F. Ranada "Knotted solutions of the Maxwell equations in vacuum", J. Phys. A: Math. Gen. 23 L815 (1990) ref] was presented explicit analytical solution as example. Let
(2.2)
In subsequent work [A.F. Ranada "Knotted solutions of the Maxwell equations in vacuum", J. Phys. A: Math. Gen. 23 L815 (1990) ref] was presented explicit analytical solution as example. Let
(2.2)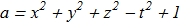 (2.3)
(2.3) (2.4)
(2.4)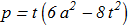 (2.5)
(2.5) (2.6)
(2.6)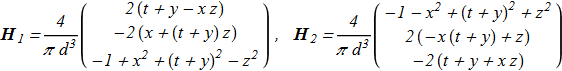 then the exact solutions of the equations (1.1)-(1.4):
(2.7)
then the exact solutions of the equations (1.1)-(1.4):
(2.7)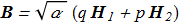 (2.8)
(2.8)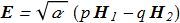 From this solution it follows
(2.9)
From this solution it follows
(2.9)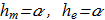 Each of the fields (2.7) and (2.8) corresponds to the Hopf fibration. The energy density:
(2.10)
Each of the fields (2.7) and (2.8) corresponds to the Hopf fibration. The energy density:
(2.10)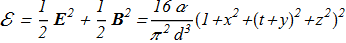 This is a finite-energy solution, but it spreads in time:
(2.11)
This is a finite-energy solution, but it spreads in time:
(2.11)
[A.F. Ranada, J.L. Trueba "Electromagnetic knots", Phys. Lett. A 202 (1995) 337 ref]
[A.F. Ranada, J.L. Trueba "Ball lightning an electromagnetic knot?", Nature 383, 32 (1996) ref]
[W.T.M. Irvine, D. Bouwmeester "Linked and knotted beams of light", Nature Physics 4, 817 (2008) ref]: the annotation will be added.
[W.T.M. Irvine "Linked and knotted beams of light, conservation of helicity and the flow of null electromagnetic fields", J. Phys. A: Math. Theor. 43 (2010) 385203 ref]: the annotation will be added.
This page is not complete and if you find inaccuracies, if you have any comments or additional material - do not hesitate to contact us.