The model is also known as the Faddeev or Faddeev-Niemi model. The model was first proposed by L.D.Faddeev in 1975 [L.D. Faddeev, "Quantization of solitons". Preprint IAS Print-75-QS70 (Inst. Advanced Study, Princeton, NJ, 1975), 32 pp. copy],[L.D. Faddeev,
"Some comments on the many dimensional solitons". Lett. Math. Phys. 1 (1976) 289-293. ref]. The hamiltonian density and energy (in the static case):
(1.1)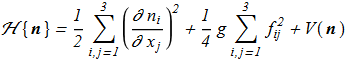
(1.2)
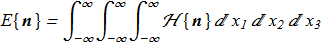in short form:
(1.3)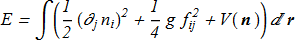
where
(1.4)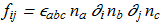
(first multiplier - Levi-Civita symbol), unit vector field
(1.5)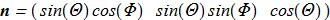
(1.6)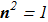
Second term in the Hamiltonian has a number of equivalent representations
(1.7)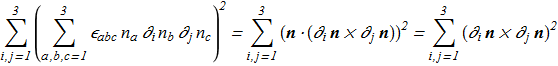
The potential term is usually in the form:
(1.8)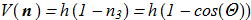
Such potential energy term causes the exponential localization of the solution. But the case V = 0 is also applicable and will assumed as default. In terms of angle variables the hamiltonian is free from the constraints:
(1.9)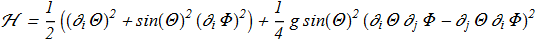
Euler-Lagrange equations
(1.10)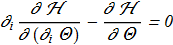
(1.11)
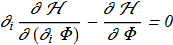describe the stationary equilibrium states. The trivial solution is
(1.12)
means a homogeneous state with minimum energy is zero.
Most complex mathematical problem is to find nontrivial analytic solutions (continuous and defined at each point in 3D space for n-vector projections) for which
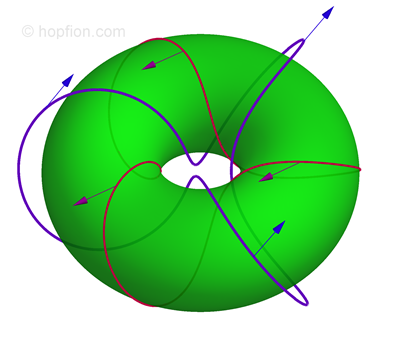
(1.13)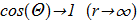
Such a solution would be a static soliton. If the Hopf index is not zero, then such soliton = hopfion.
Skyrme proposed a model [T.H.R. Skyrme "A Non-Linear Field Theory", Proc. R. Soc. Lond. A 260, 127 (1961) ref] describing hadronic physics, with the hamiltonian density
(2.1)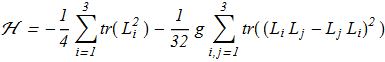
where tr() is the trace function; square matrix 2x2 are defined as follows
(2.2)
where U are also 2x2 matrix:
(2.3)
Unit vector field and the Pauli matrices vector here:
(2.4)
(2.5)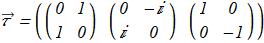
Thus, the Hamiltonian includes three angular functions (Θ,Φ,Β) are defined on the whole real space R3. In case of
Β=π/2 we immediately obtain the Hamiltonian of the Faddeev. This condition is called electroneutral "pion fluid" in the work [V.G. Makhan'kov, Yu.P. Rybakov and V.I. Sanyuk "The Skyrme model and strong interactions", Sov. Phys. Usp. 35 55 (1992) ref].
In 1979 the relationship [A.F. Vakulenko and L.V. Kapitanski, Dokl. Akad. Nauk USSR 246, 840 (1979) copy; Sov. Phys. Dokl. 24, 432 (1979).] between the full energy and the Hopf charge was found:
(3.1)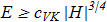
This in particular may mean that if the hopfions are separated from each other over great distances, it is energetically favorable to condense into a single hopfion. In 1981 in Russia was published a paper by Yu.P. Rybakov [Yu.P. Rybakov, "Problems of the theory of gravitation and elementary particles", vol. 12, p. 147 (1981) (in Russian). copy], where some analitical results concerning hopfions properties was found. Investigated the case of toroidal hopfions:
(3.2)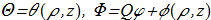
in cylindrical coordinate system (ρ,φ,z). This is the case of axial symmetry is apparently the most simple. These expressions satisfy the equations, and translate the domain from 3D to half-plane (ρ,z). For such configuration also the Hopf index can be calculated explicitly:
(3.3)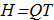
where
(3.4)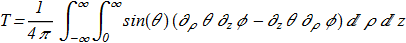
First found limit for Vakulenko-Kapitansky constant:
(3.5)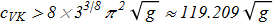
Some of these results were later published in English [A. Kundu and Yu.P. Rybakov, J. Phys. A 15, 269 (1982). ref].
New unknown functions {3.2} can be represented by a new unit vector field:
(3.6)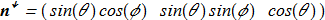
with the own topological charge T in the form
(3.7)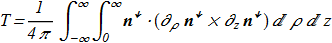
This is an integral of the Pontryagin density over half-plane.
The paper [K. Fujii, S. Otsuki and F. Toyoda "A Soliton Solution with Baryon Number B=0 and Skyrmion", Prog. Theor. Phys. Vol. 73 No. 2 (1985) pp. 524 ref, copy] identified a very useful procedure. Let we have a test configuration of the field:
(3.8)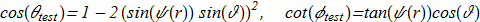
in spherical (r,θ,φ) coordinate system, and ψ(r) is a some new function which is monotonically decreasing from π to 0 at infinity. For this configuration T=1 and the structure of the 2D vector field {3.6} is a vortex:
(3.9)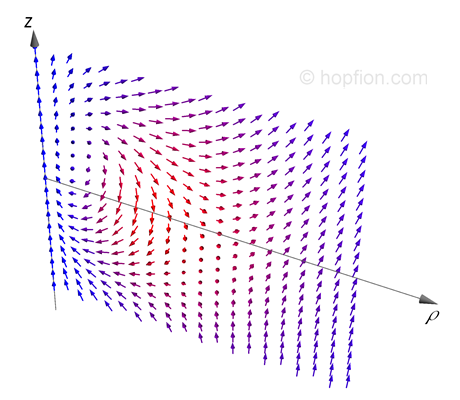
We substitute the test function into the Hamiltonian, assuming Q=1
(3.10)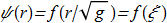
(3.11)
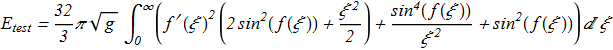The next good approximation of the solution is provided by the Atiyah-Manton trial function:
(3.12)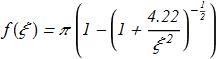
We get
(3.13)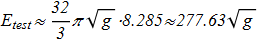
This result shows that there is a hopfion with H=1 which real energy is lower than that calculated. A similar analysis can be done for the case Q>1 i.e. for hopfions with H>1.
The Hamiltonian satisfies the simple virial test. Let
(4.1)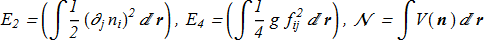
where each term is positive. For stable solutions with finite energy, we must have stability with respect to all kinds of infinitesimal perturbations, in particular
(4.2)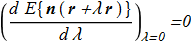
(4.3)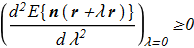
For our Hamiltonian required
(4.4)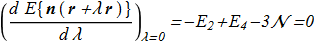
(4.5)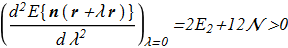
and the test passes (it's real). This is an important feature of the model lies in the fact that the Hamiltonian is not subject to the prohibition of Hobart-Derrick theorem. This fact contributes to the possibility of a numerical search for solutions by minimizing the energy functional. In addition, the ratio {4.4} can be used to verify the accuracy of the energy value of the solution found.
The revolutionary works was published in 1996. In [J. Gladikowski, M. Hellmund "Static solitons with non-zero Hopf number", arXiv:hep-th/9609035v1; Phys. Rev. D 56, 5194 (1997) ref], the authors first obtained the numerical solutions for toroidal hopfions. For H=1 and H=2 we can find the calculated energy values:
(4.6)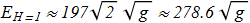
(4.7)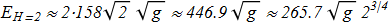
The authors also investigated the case of non-zero potential and a more complicated Hamiltonian.
In the next mounth paper [L.D. Faddeev, A.J. Niemi, "Knots and Particles", arXiv:hep-th/9610193v1; Nature 387, 58 (1997) ref], the authors also obtained the numerical toroidal hopfion H=1 for the zero potential model, but there is no energy calculation for comparison. In the article was also found not axially symmetric hopfion with H=3 - trefoil. But these calculations were done on a very coarse grid (21x21x21) and were not confirmed in the future as a credible.
[L.D. Faddeev, A.J. Niemi, "Toroidal Confugurations As Stable Solitons", arXiv:hep-th/9705176v1]: A more detailed description of the calculation of the toroidal hopfion.
[R.A. Battye and P.M. Sutcliffe "To be or knot to be?", arXiv:hep-th/9808129v1; Phys. Rev. Lett. 81 p.4798 (1998) ref]: Hopfions have been found for H=1,2,...8 (including trefoil only for H=7), energy was calculated.
[J. Hietarinta, P. Salo "Faddeev-Hopf knots: Dynamics of linked un-knots", arXiv:hep-th/9811053v1; Phys. Lett. B 451 p.60 (1999) ref]: Studied a variety of metastable states associated with the same Hopf index. In the conclusion we can find: "In particular, it would be useful to know which configurations of the same Hopf charge can be smoothly deformed to each other, and whether in such cases there exists a deformation sequence where energy always decreases". The answer is: any configurations of the same Hopf charge can be smoothly deformed to each other; this is a direct consequence of the fact that the Hopf index is unique identifier of the class in the homotopy group.
[R.A. Battye and P.M. Sutcliffe "Solitons, Links and Knots", arXiv:hep-th/9811077v1; Proc. Roy. Soc. Lond. A 455 (1999) 4305 ref]: A more detailed study of hopfions with H=1,2,...8.
[R.S. Ward "Hopf Solitons on S^3 and R^3", arXiv:hep-th/9811176v1; Nonlinearity 12 (1999) 241 ref]: proposed an improved value of the VK constant, but there is no strict mathematical proof.
[J. Hietarinta, P. Salo "Ground state in the Faddeev-Skyrme model" Phys. Rev. D 62, 081701 (2000) ref]: A detailed comparison of different configurations with the same topological index, their energies. It is noted that the soliton energy for H=2 is anomalously small.
[R.S. Ward "The Interaction of Two Hopf Solitons", arXiv:hep-th/0001017v1; Phys.Lett. B 473 (2000) 291-296 ref]: the annotation will be added.
[Fanghua Lin, Yisong Yang "The Faddeev knots as stable solitons: Existence theorems", Science in China Ser. A Mathematics 47 (2004) 187 ref]: the annotation will be added.
[Fanghua Lin, Yisong Yang "Existence of Energy Minimizers as Stable Knotted Solitons in the Faddeev Model", Commun. Math. Phys. 249, 273 (2004) ref]: the annotation will be added.
[J. Hietarinta, J. Jäykkä, P. Salo "Relaxation of twisted vortices in the Faddeev-Skyrme model", arXiv:cond-mat/0309499v1; Phys. Lett. A 321 (2004) 324-329 ref]: the annotation will be added.
[D. Auckly, L. Kapitanski "Analysis of the Faddeev model" arXiv:math-ph/0403025v1; Commun. Math. Phys. 256, 611 (2004) ref]: the annotation will be added.
[A.P. Protogenov "Knots and links in the order parameter distributions of strongly correlated systems", Phys. Usp. 49 667–691 (2006) ref]: a review article.
[P. Sutcliffe "Knots in the Skyrme-Faddeev model", arXiv:0705.1468v1; Proc. Roy. Soc. Lond. A 463 (2007) 3001 ref]: the annotation will be added.
[E. Radu and M.S. Volkov "Stationary ring solitons in field theory - knots and vortons", arXiv:0804.1357v1; Physics Reports 468, (2008) 101 ref]: a review article.
[J. Jäykkä "On Topological Solitons in The Faddeev-Skyrme Model and its Extensions" Turku 2009, copy]: Book.
[D. Harland, M. Speight, P. Sutcliffe "Hopf solitons and elastic rods", arXiv:1010.3189v1; Phys. Rev. D 83 065008 (2011) ref]: the annotation will be added.
[D. Foster "Massive Hopfions", arXiv:1012.2595v1; Phys. Rev. D 83 085026 (2011) ref]: the annotation will be added.
[J. Hietarinta, J. Palmu, J. Jäykkä, P. Pakkanen "Scattering of knotted vortices (Hopfions) in the Faddeev-Skyrme model", arXiv:1108.5551v1 (2011); New J. Phys. 14 (2012) 013013 ref]: Dynamics of hopfions in action! Time evolution was computed using Runge-Kutta method for non-static Lagrangian. The process of connecting the singly charged hopfions has been investigated: video1, video2.
This page is not complete and if you find inaccuracies, if you have any comments or additional material - do not hesitate to contact us.