Bose-Einstein condensate is described by the Gross-Pitaevskii equation. Consider the Hamiltonian density, which was proposed in [T.L. Ho "Spinor Bose Condensates in Optical Traps", arXiv:cond-mat/9803231v1; Phys. Rev. Lett. 81, 742 (1998) ref]:
(1.1)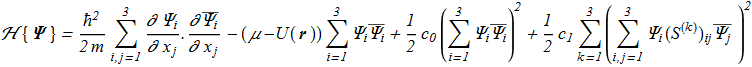
where:
(1.2)
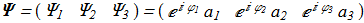is a vector of three complex variables and spin-1 matrices
(1.3)
Euler-Lagrange equations:
(1.4)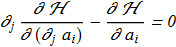
(1.5)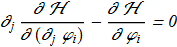
The solution of equations corresponding to the so-called "polar" phase:
(1.6)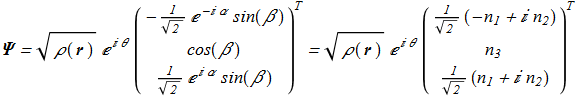
(1.7)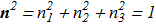
with equation on amplitude
(1.8)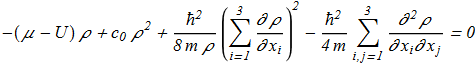
But also the solution exists where the n-vector field is not homogeneous in space:
(1.9)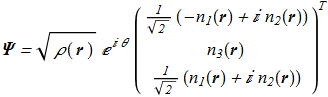
(1.10)
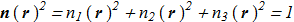with 3 partial differential equations from {1.4}-{1.5} for ρ and two n-vector parametrizing angles. The corresponding Hamiltonian density:
(1.11)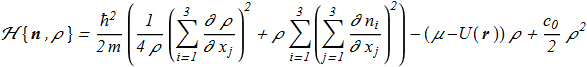
If we introduce the definition
(1.12)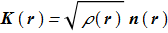
we get
(1.13)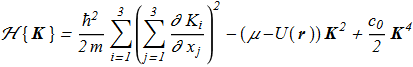
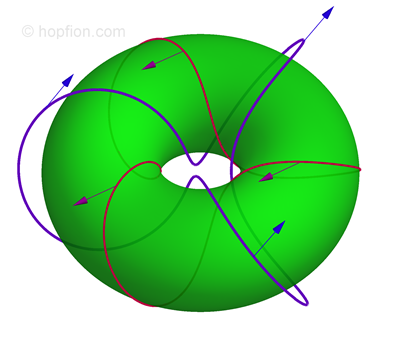
The appearance of a unit vector field in the Hamiltonian leads to some speculations [Y. Kawaguchi, M. Nitta, M. Ueda "Knots in a Spinor Bose-Einstein Condensate", arXiv:0802.1968v1; Phys. Rev. Lett. 100, 180403 (2008) ref], [Y. Kawaguchi, M. Kobayashi, M. Nitta, M. Ueda "Topological Excitations in Spinor Bose-Einstein Condensates", arXiv:1006.5839v1; Prog. Theor. Phys. Suppl. 186 (2010) 455, ref] about the existence of knots with nonzero Hopf index. However, the presence of the scalar density in {1.11} can not be simply discarded. The constant value ρ=const does not correspond to an extremum of the Hamiltonian {1.11} with non-homogeneous n-field. Instead of map
(2.1)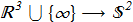
we have a map for {1.13}
(2.2)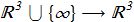
which is homotopic to zero. Any configuration of the n-field can be cutted into regions with zero vector amplitude (ρ=0), and each knot for n-field can be destroyed, while the original function {1.2} can be continuous. This fact means that even if the parametric space are include some Hopf fibration, it is not topologically stable knot, it is not a hopfion in the strict mathematical sense.
Similar problems arise for other representations of the energy functionals, such as [E. Babaev, L.D. Faddeev, A.J. Niemi "Hidden symmetry and knot solitons in a charged two-condensate Bose system", arXiv:cond-mat/0106152v1; Phys. Rev. B 65 100512 (2002) ref].
This page is not complete and if you find inaccuracies, if you have any comments or additional material - do not hesitate to contact us.