There are many magnetic crystals without an inversion center, where exchange-relativistic interactions lead to the formation of long-period magnetic structures whose periods are significantly longer than interatomic distances. These structures are spirals and helicoids of a certain chirality. Such materials are commonly called chiral magnets or incommensurate magnets. In [V.G. Bar'yakhtar and E.P. Stefanovsky Fiz. Tverd. Tela 11, 1946 (1969) copy; Sov. Phys. Solid State 11, 1566 (1970)], [P. Bak and M.H. Jensen "Theory of helical magnetic structures and phase transitions in MnSi and FeGe", J. Phys. C 13 L881 (1980) ref] was proposed the energy functional
(1.1)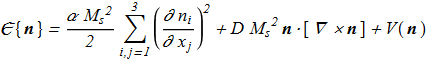
(1.2)
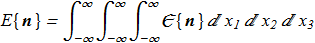In [A. Bogdanov "New localized solutions of the nonlinear field equations", JETP Lett. 62, 247 (1995) ref] was proved that Hobart-Derrick theorem does not prohibit the existence of three-dimensional localized solutions for the energy functional {1.1}. The main difference between this model from "Heisenberg model" and "Uniaxial model" that it admits the possibility of a completely static three-dimensional solitons.
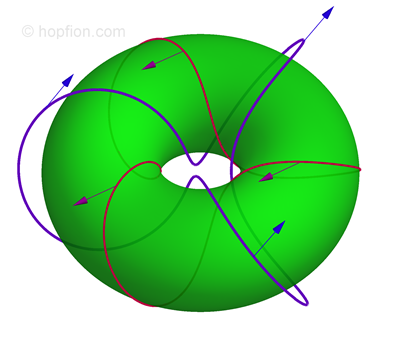
In [A.B. Borisov, F.N. Rybakov "Three-dimensional static vortex solitons in incommensurate magnetic crystals", Low Temp. Phys. 36, 766 (2010) ref; arXiv:1108.4330v1], the authors found numerically static solutions with total Hopf index equal to zero, but the structure consists of pairs "hopfion-antihopfion". Found structures are unstable to some perturbations, because they are solutions of a saddle type, and not local minima. Later authors have reported [A B. Borisov, F.N. Rybakov "Three-dimensional solitons in incommensurate ferromagnets", Int. Workshop "Spin Chirality and Dzyaloshinskii-Moriya Interaction" DMI 2011, St.-Petersburg (2011), Progr. and Abstr., p.40 , ref] on the results of calculations of toroidal hopfion-type texture. But it is also unstable to some perturbations and, therefore, is not a true hopfion.
Numerical simulations shows that hopfion-type textures can be stabilized in confined geometries - films and discs of chiral magnet with additional artificial layers on top/bottom surfaces responsible for pinning of spins [J.-S.B. Tai, I.I. Smalyukh "Hopf solitons and knotted emergent fields in solid-state non-centrosymmetric magnets" arXiv:1806.00453v1, Phys. Rev. Lett. 121, 187201 (2018) ref], [Y. Liu, R. Lake, J. Zang "Binding a Hopfion in Chiral Magnet Nanodisk" arXiv:1806.01682v1, Phys. Rev. B 98, 174437 (2018) ref], [P. Sutcliffe "Hopfions in chiral magnets", arXiv:1806.06458v1, Journal of Physics A 51, 375401 (2018) ref], see also [X. S. Wang, A. Qaiumzadeh, A. Brataas "Current-Driven Dynamics of Magnetic Hopfions", arXiv:1905.09154v1, Phys. Rev. Lett. 123, 147203 (2019) ref]. Such textures are of some interest, but however, are not canonical hopfions, because stability is due to the geometrical confinement, while three-dimensional solitonic features (i.e. ability of motion, collisions and also other features inherent for particle-like states) are impossible in principle. The following name more accurately reflects the essence of the mentioned textures: the imprinting of Hopf fibration.
The hopfion solutions for chiral magnet were demonstrated in [J.-S.B. Tai, I.I. Smalyukh "Three-dimensional crystals of adaptive knots", Science 365, 1449 (2019) ref, arXiv:1911.09160v1]. Despite the work is devoted to liquid crystals, there is a certain correspondence between the Hamiltonians. Thus, some of the numerical results are directly related to chiral magnets. A more focused on chiral magnets study was published later [R. Voinescu, J.-S.B. Tai, I.I. Smalyukh "Hopf solitons in helical and conical backgrounds of chiral magnetic solids", arXiv:2004.10109v1, PRL 125, 057201 (2020) ref]. These works provide convincing theoretical data on the stability of hopfions in chiral magnets. The particles are stable at low magnetic fields, where the ground state is a helicoidal/conical phase. The particles are capable of moving in all three dimensions, although the motion along the modulation direction of the background is rather nontrivial. The experimental challenge of their nucleation and observation seems to be difficult but is extremely interesting.
This page is not complete and if you find inaccuracies, if you have any comments or additional material - do not hesitate to contact us.