
The Euler equations of motion of an ideal liquid:
(1.1)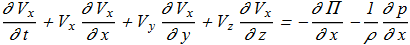 (1.2)
(1.2)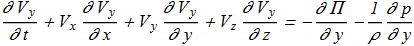 (1.3)
(1.3) The potential of body forces
(1.4)
The potential of body forces
(1.4)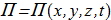 Consider a barotropic fluid flow
(1.5)
Consider a barotropic fluid flow
(1.5)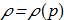 i.e. density of the liquid depends only on the pressure
(1.6)
i.e. density of the liquid depends only on the pressure
(1.6)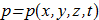 We introduce the definition for vorticity
(1.7)
We introduce the definition for vorticity
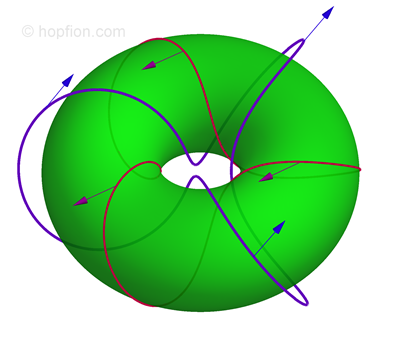
(1.7)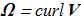 In 1961 it was shown [J.-J. Moreau, Comptes rendus de l'Académie des Sciences 252, 2810 (1961) copy] that for the equations (1.1)-(1.3) with condition (1.5), the integral named helicity
(1.8)
In 1961 it was shown [J.-J. Moreau, Comptes rendus de l'Académie des Sciences 252, 2810 (1961) copy] that for the equations (1.1)-(1.3) with condition (1.5), the integral named helicity
(1.8)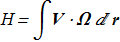 (for the flow with good boundary conditions at infinity) remains a constant
(1.9)
(for the flow with good boundary conditions at infinity) remains a constant
(1.9)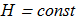 Indeed, it is easy to verify the identity
(1.10)
Indeed, it is easy to verify the identity
(1.10)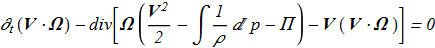 by substituting the time-derivatives of the velocity V from (1.1)-(1.3). From (1.8) and (1.10) it follows that if the motion is localized in space (the velocity decreases rapidly at infinity), then (1.9).
by substituting the time-derivatives of the velocity V from (1.1)-(1.3). From (1.8) and (1.10) it follows that if the motion is localized in space (the velocity decreases rapidly at infinity), then (1.9).
Later, the same conclusions were reached by Moffat [H.K. Moffat "The degree of knottedness of tangled vortex lines", J. Fluid Mech. 35 (1969), 117 ref]. He also described the meaning of the topological invariant (1.8) although apparently he did not know about the direct relationship with the Hopf fibration [H.Hopf "Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche", Math. Annalen 104 (1931), 637 ref] and about Whitehead expression [J.H.C. Whitehead "An expression of Hopf’s invariant as an integral", Proc. Nat. Acad. Sci. U.S.A. 33 (1947), 117 ref].
Direct indication that the flow with nonzero H are hopfions has been done in [E.A.Kuznetsov, A.V. Mikhailov "On the topological meaning of canonical Clebsch variables", Phys. Lett. A 77 (1980), 37 ref]. In this work has been defined a direct relationship between the vectors and the n-field and the Clebsch variables;
(1.11)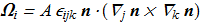
A topological invariant H follows directly from the Euler equations, but for the physically correct solution of the system, we need an additional relationship - continuity equation:
(1.12)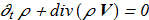
In [E. A. Kuznetsov, V. P. Ruban "Collapse of vortex lines in hydrodynamics", JETP 91 (2000), 775 ref] reported that one of the simplest initially hopfion flow of an incompressible fluid
(2.1)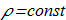 leads to the collapse of type
(2.2)
leads to the collapse of type
(2.2)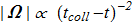
This page is not complete and if you find inaccuracies, if you have any comments or additional material - do not hesitate to contact us.